Math Quiz - Series 4 | Test your skills with Engineering Math Quiz. Answers and solutions provided!

• Series 4

Math Series 4

---

1. Find the first three terms of the Taylor series for f(x) = cos(5x) at x = 0.

1. 1 + x - 25 x^2 /2
2. 1 - 25x/2 + x^2
3. 1 - 25 x^2 /2
4. 1 - 25x/2

Answer: C
Solution:

Taylor Series:
$$ f(x) = \sum_{k=0}^\infty \frac{(x - x_0)^k}{k!} f^k (x_0) $$ $$\begin{align} x_0 & - \text{ initial guess} \\ f^k & - \text{ kth derivative of $f(x)$ at $X = X_0$} \\ \end{align}$$

@ x ₀ = 0, $$\begin{align} f(x) & = cos(5x) \to f(0) = 1 \\ f'(x) & = -5 \sin (5x) \to f'(0) = 0 \\ f"(x) & = -25 \cos (5x) \to f"(0) = -25 \\ \end{align}$$ $$\begin{align} f(x) & = \frac{(x-0)^0}{0!} \cdot 1 + \frac{(x-0)^1}{1!} \cdot 0 + \frac{(x-0)^2}{2!} \cdot (-25) \\ & = 1 - \frac{25}{2}x^2. \end{align}$$

---

2. The first Newton approximation x₁ for a zero f(x) = x^3 - 2x with initial approximation x₀ = 2.

1. 3/5
2. 3/7
3. 8/7
4. 8/5

Answer: D
Solution:

Newton-Raphson Method
$$ X_{n+1} = X_n - \frac{Y_n}{Y'_n} $$

Solving for y and y'. $$\begin{align} y & = x^3 - 2x \\ y' & = 3x^2 - 2 \\ \end{align}$$ Solving for the 1st iteration at X₀ = 2, $$\begin{align} X_{n+1} & = X_n - \frac{X_n^3 - 2 X_n}{3X_n^2 - 2} \\ X_1 & = (2) - \frac{2^3 - 2(2)}{3(2)^2 - 2} \\ & = \frac{8}{5} \\ \end{align}$$

---

3. Write the converse of the statement, "If Maria Hill finishes her work, she will go to the basketball game."

1. If Maria Hill goes to the basketball game, she will not finish her work.
2. If Maria Hill goes to the basketball game, she will finish her work.
3. If Maria Hill will not go to the basketball game, she will finish her work.
4. If Maria Hill will not go to the basketball game, she will not finish her work.

Answer: B
Solution:

Implication $$ p \to q \text{ or "If p, then q."}$$ Converse $$ q \to p \text{ or "If q, then p."}$$ Inverse $$ -p \to -q \text{ or "If not p, then not q."}$$ Contrapositive $$ -q \to -p \text{ or "If not q, then not p."}$$

The converse of the statement "If Maria Hill finishes her work, she will go to the basketball game." is "If Maria Hill goes to the basketball game, she will finish her work."

---

4. Divide 24 into three parts such that the continued product of the first part, the square of the second part, and the cube of the third part is maximum.

1. x = 12, y = 8, z = 4
2. x = 14, y = 6, z = 4
3. x = 10, y = 8, z = 6
4. x = 16, y = 6, z = 2

Answer: A
Solution:
x, y, z as three parts of 24: $$ x + y + z = 24 \text{ (Eq. 1)}$$ Product, $$P = zy^2x^3 \text{ (maximum)}$$
Substuting Eq. 1 to P, $$P = (24-x-y)y^2x^3$$

If the equation of the quantity with unknown max. or min. value have more than two variables, get the partial derivative and equate to zero.

$$ \frac{\partial P}{\partial x} = \frac d{dx} \left( (24-x-y)y^2x^3 \right) = 0 $$ By subsituting values from choice A and using your calculator, x = 12, y = 8, $$ \begin{align} & \begin{array}{c|c} \frac d{dx} \left[ (24-x-y)y^2x^3 \right] & _{x=12} \\ & _{y=8} \\ \end{array}\\ & = 0. \\ \end{align} $$

---

5. What is the integrating factor of the differential equation (1 + x^2)dy/dx + 2xy = cos x ?

1. 1 + x²
2. 1/(1+x²)
3. log (1+x²)
4. log (x²)

Answer: A
Solution:

1st Order Linear Differential Equation $$ \frac {dy}{dx} + P(x)y = Q(x) $$ $$ I.F. = e^{\int Pdx}$$ Bernoulli's Differential Equation $$ \frac {dy}{dx} + P(x)y = Q(x)y^n $$ $$ I.F. = e^{(1-n) \int Pdx}, n \neq 0.1$$ Non-exact Differential Equation $$ M(x,y)dx + N (x,y)dy = 0, \frac{\partial M}{\partial y} \neq \frac{\partial N}{\partial x} $$ $$ I.F. = e^{\int Pdx}$$ $$ P = \frac{ \frac{\partial M}{\partial y} - \frac{\partial N}{\partial x} }{N}$$

From the given, it can be seen that the D.E. is a 1st Order Linear D.E.: $$ \begin{align} (1 + x^2) \frac{dy}{dx} + 2xy & = \cos x \\ \frac{dy}{dx} + \frac{2xy}{1+x^2} & = \frac{\cos x}{1+x^2} \to \text{ 1st Order Linear D.E.} \\ \end{align} $$ $$ P = \frac{2x}{1+x^2} $$ $$\begin{align} I.F. & = e^{\int P dx} \\ & = e^{\int \frac{2x}{1+x^2} dx} \\ \\ \int \frac{du}{u} & = \ln (u) + c \\ u & = 1 + x^2 \\ du & = 2x dx \\ \\ I.F. & = e^{\ln (1+x^2)} \\ & = 1 + x^2. \end{align} $$

---

6. The singular point of the differential equation (1-x²) d²y/dx² - 2x dy/dx + n(n+1)y = 0 is _____.

1. x = 0
2. x = ±1
3. x = 1
4. x = 2

Answer: B
Solution:

To get the singular point of a D.E., let the term with the highest derivative equal to zero. Singular Point is the maximum or minimum point and a critical point of 2nd degree D.E. and higher.

From the given, $ (1-x^2) \frac{d^2y}{dx^2} - 2x \frac{dy}{dx} + n (n+1)y = 0$ the term with the highest derivative: $$\begin{align} (1-x^2) \frac{d^2y}{dx^2} & = 0 \\ 1 - x^2 & = 0 \\ x^2 & = 1 \\ x & = \pm 1 \\ \end{align}$$

---

7. y = e^x is a part of C.F. of differential equation d²y/dx² + P dy/dx + Qy = 0 if ______.

1. 1 + P + Q = 0
2. P + Qx = 0
3. 1 - P + Q = 0
4. P - Qx = 0

Answer: A
Solution:

A complementary function is the general solution of homogenous, linear differential equation. Solving the auxiliary equation, gives the value of root m which is needed to find the complementary function. There are three possible complementary solutions (depending on the roots of the auxiliary function):

• Case 1: m are real and distinct ($b^2 > 4ac$) $$ y = C_1 e^{m_1 x} + C_2 e^{m_2 x} + ... $$
• Case 2: m are real and equal ($b^2 = 4ac$) $$ y = C_1 e^{m_1 x} + C_2 x e^{m_2 x} $$
• Case 3: m is complex, m = a + bi ($b^2 < 4ac$) $$ y = e^{ax} ( C_1 \cos bx + C_2 \sin bx ) $$

To get the auxiliary equation, let $$ y = e^{mx} $$ $$ \frac{dy}{dx} = me^{mx} $$ $$ \frac{d^2y}{dx^2} = m^2 e^{mx} $$ or in short, $$ \frac{d^n y}{dx^n} \Rightarrow m^n $$

From the given, the auxiliary equation is: $$\begin{align} \frac{d^2 y}{dx^2} + P \frac{dy}{dx} + Qy & = 0 \\ m^2 + P m^1 + Q m^0 & = 0 \\ m^2 + P m + Q & = 0 \\ \end{align}$$ As $y = e^x$ is part of the solution, using Case 1, $$\begin{align} e^x & = C_1 e^{mx}\\ x & = m x \\ m & = 1\\ \end{align}$$ Substiuting m, $$\begin{align} m^2 + P m + Q & = 0 \\ (1)^2 + P(1) + Q & = 0 \\ 1 + P + Q & = 0\\ \end{align}$$

---

8. The volume of the tetrahedron bounded by the co-ordinate planes and the plane x + y + z = 4 is equal to ____.

1. 32/3
2. 4/3
3. 16/3
4. 128/3

Answer: A
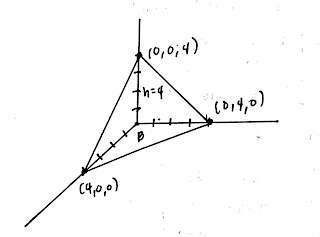
Solution:

$$\begin{align} V_{(tetrahedron)} & = V_{(pyramid)} \\ & = \frac{1}{3}Bh \\ & = \frac{1}{3} (\frac{1}{2} \cdot 4 \cdot 4) \cdot 4 \\ & = \frac{32}{3} \end{align}$$

---

9. The area bounded by the curve xy = 4, y axis, and the lines y = 1 to y = 4 is given by ____.

1. 2 log 2
2. 8 log 2
3. 4 log 2
4. 16 log 2

Answer: B
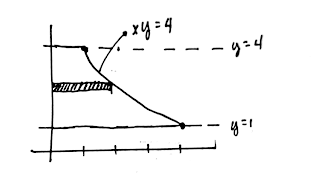
Solution:

$$\begin{align} Area & =\int_{Y_1}^{Y_2}(X_R - X_L) dy \\ & = \int_1^4(\frac{4}{y}-0) dy \\ & = 8 \ln 2 \\ \end{align}$$

---

10. If the base radius and height of a cone are measured as 4 and 8 with a possible error of 0.04 and 0.08 inches, respectively, calculate the percentage of error in calculating the volume of the cone.

1. 1%
2. 3%
3. 2%
4. 4%

Answer: B
Solution:

$$\begin{align} V_(cone) & = \frac{1}{3}Bh \\ & = \frac{1}{3} \pi r^2 h \\ \end{align}$$ initial volume: r = 4, h = 8, $$\begin{align} V_i & = \frac{1}{3} \pi (4)^2 (8) \\ & = \frac{128}{3} \pi \\ \end{align}$$ final volume: r = 4 + 0.04, h = 8 + 0.08, $$\begin{align} V_f & = \frac{1}{3} \pi (4+0.04)^2 (8+0.08) \\ & = \frac{2060602}{46875} \pi \\ \end{align}$$ $$\begin{align} \text{% change} & = \frac{V_f - V_i}{V_i} \times 100 \\ & = 3 \% \\ \end{align}$$

---